9. In metallic iron, the atoms are arranged at the corners and the center of a cube of edge 2.866 Å, in the same body-centered cubic structure shown in this chapter for lithium. What is the volume of this unit cube, and how many iron atoms are there per unit volume of this size? (Be careful. If an iron atom is shared between four unit volumes, then only one quarter of the atom can be counted for a given unit volume. What is the situation with regard to sharing for one of the atoms at the corners of the cube? What about the atom in the center of the cube?)

10. What is the atomic volume for iron, in Å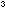 per atom? What is the atomic density, in atoms per Å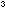? How many atoms are there per cubic centimeter in iron?

11. The measured density of iron is 7.86 g cm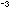. If the atomic weight of iron is 55.85, how many moles of iron are there per cubic centimeter?

12. Use the answers to Problems 10 and 11 to obtain an experimental value for Avogadro's number. How does it compare with the value that we have used before?

13. The structure of crystalline sodium chloride can be thought of as being built from cubes with 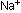and 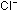ions on alternating corners, as in the diagrams seen previously in this chapter. The distance between the centers of 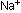and 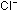ions along an edge of the cube is 2.820 Å. (These crystal spacings can be obtained from x-ray diffraction experiments.) How many NaCl units are there in a cube 2.820 Å on a side? (Remember the sharing of ions with several adjacent cubes. You should come up with an answer of one half unit of NaCl per cube of edge 2.820 Å.) What is the density of sodium chloride, in NaCl pairs per Å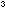? What is the density in NaCl pairs per cm?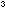

14. The measured density of rock salt is 2.165 g cm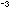. Calculate the molecular weight of NaCl from the atomic weights on the inside back cover, and calculate the density of NaCl in
moles cm.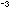

15. Use your answers to Problems 13 and 14 to calculate Avogadro's number. How does it compare with the value we have been using?