|
These values for 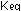 ,
raise some paradoxical questions. At 2300K inside the combustion
chamber, appreciable amounts of NO will be formed from ,
raise some paradoxical questions. At 2300K inside the combustion
chamber, appreciable amounts of NO will be formed from 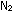 and
and 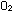 from the intake of air.
from the intake of air.
Example. At equilibrium a 1-liter steel tank at 2300K contains
0.04 mole of 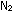 ,
0.01 mole of ,
0.01 mole of 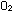 ,
and an unknown amount of NO. How many moles of NO are present, and
what is the mole fraction of NO? ,
and an unknown amount of NO. How many moles of NO are present, and
what is the mole fraction of NO?
Solution. The equilibrium-constant expression for the reaction
is:
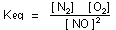
 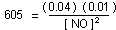
[NO] = 0.00081 mole liter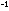
total moles = 0.04 + 0.01 + 0.0008 = 0.0508
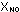 = 0.0008 / 0.0508 = 0.016
= 0.0008 / 0.0508 = 0.016
The hot engine gases thus are 1.6% (mole percent) NO, which is an
appreciable amount. However, if we repeat the calculations of the
preceding example, but at room temperature, we arrive at the paradoxical
conclusion that NO should be no problem in air pollution; equilibrium
at 298K fies far on the side of 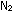 and and
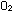 : :
|
|
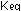 = 2.20 x 10
= 2.20 x 10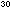
[NO] = 5.2 x 10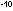 mole liter
mole liter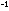 within the steel tank.
within the steel tank.
This quantity of NO would be totally undetectable and unimportant.
Where is the flaw in the analysis? The oxide NO obviously is a serious
problem in photochemical smog. It is produced at high temperatures
in internal combustion engines, but why does it not break down spontaneously
into 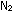 and
and 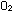 as the gases rush out the tailpipe and are cooled down?
as the gases rush out the tailpipe and are cooled down?
The problem is one of rates of reaction, and not of equilibrium.
True, NO at equilibrium at 298K should break down into 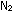 and
and 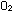 ,
but the gases in our atmosphere are far from equilibrium. The breakdown
reaction is a very slow one, and NO remains intact long enough to
be oxidized to ,
but the gases in our atmosphere are far from equilibrium. The breakdown
reaction is a very slow one, and NO remains intact long enough to
be oxidized to 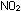 and enter the smog-producing pathway. Rates of reaction are important,
and "How fast?" often is a more important question than "How far?".
and enter the smog-producing pathway. Rates of reaction are important,
and "How fast?" often is a more important question than "How far?".
"How fast?" is the question to be considered in the following chapter.
|