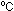Example. An eight-foot diameter weather balloon is filled with 7600 liters of at 1atm pressure and 25. How many moles of hydrogen gas are present?

Solution. P = 1 atm, V = 7600 liters, T = 25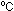 = 298K.




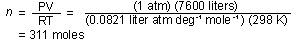
As an interesting sidelight, we can calculate the lifting power of the balloon.

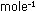Solution. The 311 moles of gas weigh 311 moles X 2.016 g = 627 g. The lifting power of the balloon is the difference between this and the weight of the air that the balloon displaces.

The same volume of air also would contain 311 moles (Avogadro's principle), and air can be considered a mixture of 80% nitrogen gas and 20% oxygen gas.

The average molecular weight of the air mixture then is

80 % x 28.013 g 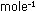+ 20 % x 32.000 g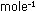
=28.81 g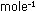

The weight of air displaced is

311 moles x 28.81 g 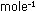= 8960 g

The buoyancy of the balloon is the difference in weight of air and hydrogen:

8960 g - 627 g = 8333 g

The balloon therefore can lift slightly more than 8 kilograms, or 18 pounds, of payload. We now can take into account the simultaneous change of pressure and temperature, and correct the flaw in the weather balloon example first used to illustrate Boyle's law.