|
The only allowed orbits were those for which the total circumference
was an integral number, n, of wavelengths:
 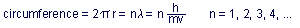
Each of these allowed orbits, or states, was called a quantum state,
characterized by a quantum number, n, which was a positive integer.
If you write the expression for the balance between electrostatic
attraction and centrifugal force for a stable orbit, and include
the restriction among radius, mass, and speed given by the above
equation, you can obtain expressions for the radii of the allowed
quantum orbits (r) and the energies of the electrons in them (E).
The sizes of the allowed orbits are given by
 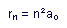
in which  is the radius of the nth permitted orbit, and
is the radius of the nth permitted orbit, and 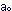 is a collection of physical constants, which for the hydrogen atom
has a numerical value of 0.53
is a collection of physical constants, which for the hydrogen atom
has a numerical value of 0.53 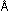 .
The size of the radius increases as the square of the quantum number;
thus the smallest (and lowest-energy) orbit has a radius of 0.53 .
The size of the radius increases as the square of the quantum number;
thus the smallest (and lowest-energy) orbit has a radius of 0.53
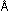 ,
the next has a radius of 2.12 ,
the next has a radius of 2.12 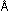 ,
and so on. These orbits are illustrated on page 26. ,
and so on. These orbits are illustrated on page 26.
|
|