Derivation of the forumla
The energy of an atom or molecule when subjected to a magnetic field B can be expressed
as the scalar product
E = - m.B
which serves to define its magnetic moment m. The origin of a magnetic moment
lies in the circulation of charge, i.e. in current loops, within the atom or
molecule. Obviously, there is a magnetic moment due to the orbital motion of electrons,
which can be written as
m = - (e/2me)I
where I is the orbital angular momentum of an electron, and me is the
mass of the electron.
One basis for the above equation is the study of the magnetic fields due to
current-bearing coils in the laboratory. The minus sign reflects the negative charge of the
electron. If we implicitly recognise the atomic unit of angular momentum, namely
h/2 , then the magnetic moment can be recast
in the simple form
, then the magnetic moment can be recast
in the simple form
m = - 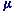 BI
BI
where I is now regrarded to be dimensionless, and
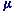 B = eh/4
B = eh/4 me
is the Bohr magneton (SI Units), the atomic unit of magnetic moment.
me
is the Bohr magneton (SI Units), the atomic unit of magnetic moment.
The spin motion of an electron (its intrinsic angular momentum s) also
gives rise to a magnetic moment, analogous in form to the orbital moment. A variety of
spectroscopic measurements have shown that the magnetic moment is given by
m = - g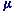 Bs
Bs
where s is the spin angular momentum and g, known as the spin g-factor,
is a numercial constant with a value of almost exactly 2. In a many electron system, the
magnetic moment is similarly proportional to the total spin angular momentum S.
The magnetic susceptibility is defined as the magnetic moment induced by unit applied
magnetic field per unit of quantity of material. It can be established by use of elementary
molecular statistics that the molar magnetic susceptibility of an ensemble of non-interacting
atoms or molecules is given by
| Xmol = |
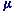 0Nm2 0Nm2 |
 |
| 3kT |
where N is the Avogadro number, k the Boltzmann constant, and 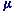 0
the vacuum permeability.
0
the vacuum permeability.
The essential result, that the susceptibility varies inversely as temperature T,
explains the time-honoured Curie Law.
In general, both the orbital and spin motions contribute to experimental magnetic moments.
However, in the case of transition metal complexes, it turns out that the electrons in d-orbitals
interact so strongly with the ligand field that their orbital magnetic moments fail
to respond to an external magnetic field; their orbital angular momentum is said to be quenched.
But the spin motion of the d electrons is essentially unaffected by the ligand field, and
so responds fully to the applied magnetic field. The result is that the magnetic moments of transition
metal complexes are largely determined by the spin state of the metal ions.
Now |S| = [S(S+1)]1/2, where S is the total spin quantum number. If n
is the number of unpaired electrons in the d shell then S = n/2, and so S = 1/2[n(n+2)]1/2.
The spin magnetic moment is therefore
m = [n(n+2)]1/2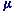 B
B
which is the formula given on the left. Actually the orbital contribution to the magnetic moment
is never completely quenched, and accurate measurements on paramagnetic nickel(II) complexes invariably yield
magnetic moments slightly larger than the "spin-only" values.
