|
If we go a little farther in thermodynamics
than this book will, it is not hard to prove the logarithmic relationship
between 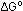 and and
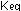 . In the equation
above In is the natural logarithm, not log . In the equation
above In is the natural logarithm, not log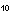 ,
or logarithm to base 10. R is the gas constant discussed in Chapter
2, with a numerical value of 1.987 cal deg ,
or logarithm to base 10. R is the gas constant discussed in Chapter
2, with a numerical value of 1.987 cal deg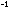
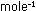 or 0.08205
liter atm deg or 0.08205
liter atm deg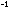
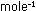 . It also
is Avogadro's number times the Boltzmann constant, k, of Chapter
13. The superscript zero on . It also
is Avogadro's number times the Boltzmann constant, k, of Chapter
13. The superscript zero on 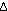 G
indicates that the free energy change in this equation is the standard
free energy change of the reaction-the value at the given temperature
when all gases are at G
indicates that the free energy change in this equation is the standard
free energy change of the reaction-the value at the given temperature
when all gases are at
|
|
one atmosphere partial pressure
and all solution components are at concentrations of one mole per
liter. In contrast, 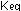 is the ratio of products to reactants at equilibrium, which
may be quite different from standard conditions. The equation above
compares the strength of the drive toward equilibrium from the standard
state, with the ratio of products to reactants once equilibrium
is attained. The more that equilibrium is skewed toward an excess
of products (large
is the ratio of products to reactants at equilibrium, which
may be quite different from standard conditions. The equation above
compares the strength of the drive toward equilibrium from the standard
state, with the ratio of products to reactants once equilibrium
is attained. The more that equilibrium is skewed toward an excess
of products (large 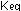 ),
the greater the initial impetus of movement (large negative ),
the greater the initial impetus of movement (large negative 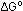 )
if the reaction is begun from standard concentrations. )
if the reaction is begun from standard concentrations.
|